2024 상문고 1학년 중간고사로 알아보는 중학교 수학의 중요성
- 001.png [File Size:670.3KB]
- 002.png [File Size:834.2KB]
- 003.png [File Size:564.9KB]
- 004.png [File Size:819.8KB]
- 005.png [File Size:773.3KB]
- 006.png [File Size:841.7KB]
- 007.png [File Size:1006.9KB]
- 프레젠테이션1.png [File Size:396.0KB]

얼마 전 상문고 중간고사가 끝났습니다. 수학 과목의 경우 평소 꾸준히 공부해온 학생이라면 16번 정도까지는 큰 무리 없이 풀 수 있었을 것입니다. 그런데, 객관식 최후반부 문항들과 서술형 문제들에 다다라서 갑자기 어려움에 봉착했던 학생들이 제법 있습니다.
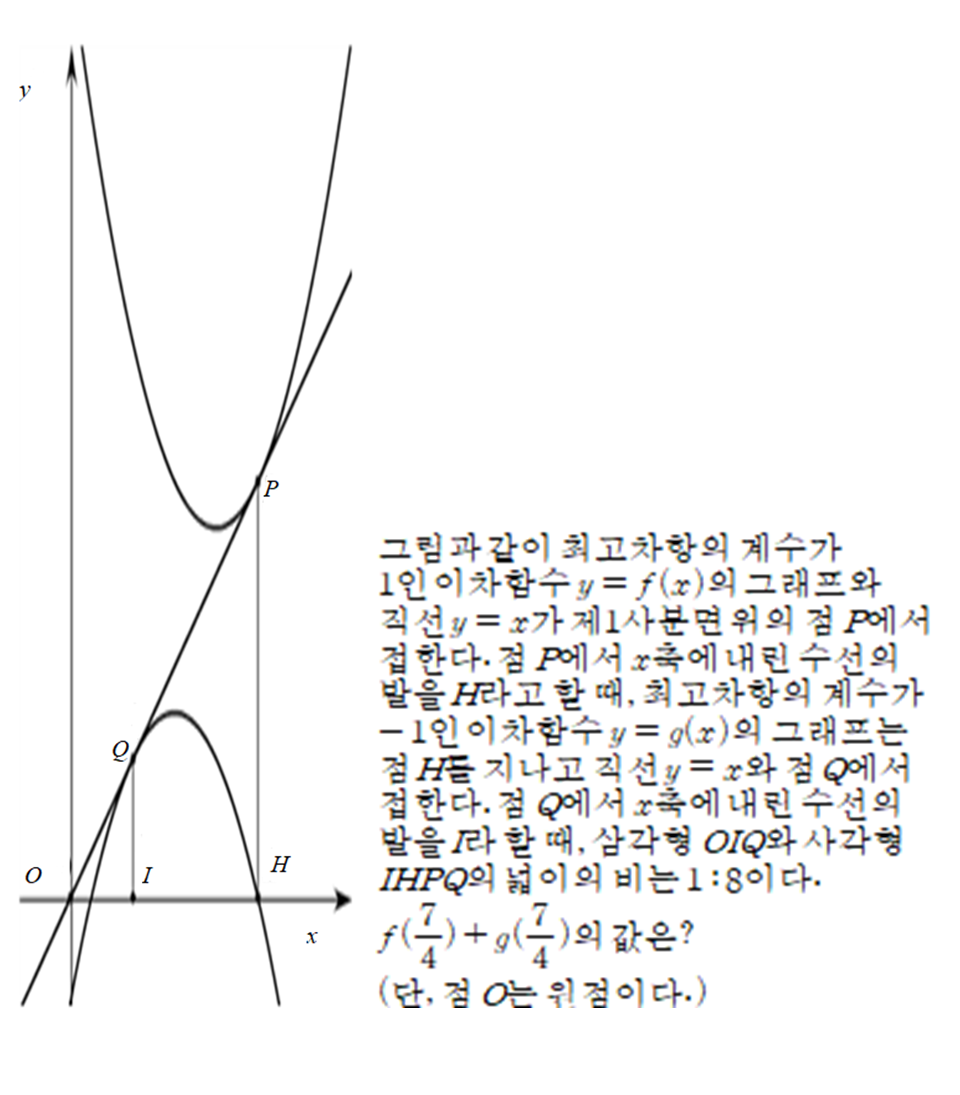
멘토들이 주목한 것은 19번 문제였습니다. 먼저 수학 시험지를 훑어보며 어떤 순서에 따라서, 어떤 문제에 얼마 정도의 시간을 안배하여 시험에 응할 것인지를 계획한 학생이라 하더라도 실제 문제풀이가 한 번이라도 자신의 예상과 다르게 흘러가기 시작한다면 페이스를 유지하기 쉽지 않습니다. 이때, 상당수 학생들에게 서술형 문제로 넘어가기 직전의 마지막 객관식 문제였던 19번은 순간의 판단 실수로 인해 페이스가 무너지는 기점이 될 가능성이 컸습니다.
위에서 19번 문제가 페이스를 무너뜨릴 수 있다고 쓴 이유는 다음과 같습니다. 문제를 읽으며, 문제에서 주어지는 조건들을 눈에 들어오는 조건들을 우직하게 다항식으로 정리한다고 해봅시다. 예컨대 처음에는 “최고차항의 계수가 1인 이차함수 y=f(x)”라는 구절을 읽으며 ‘f(x)=x^2+ax+b’라고 적는 식으로 말입니다. 이와 같이 접근하는 학생은 연후 ‘g(x)=-x^2+cx+d’라고 적을 것이고, 이후 점 P, Q의 x축 좌표 p, q도 각각 x=f(x). x=g(x)를 만족하는 미지수로 상정한 뒤 마지막에는 삼각형 OIQ와 사각형 IHPQ의 넓이의 비에 관한 조건을 활용해 8*1/2*q*g(q)=1/2*{g(q)+f(p)}*(p-q)라는 등식을 세울 것입니다. 아울러 g(p)=0이라는 조건도 활용해야 하겠지요.
그나마 간략히 적는다고 적어 보았는데, 그래도 벌써 제법 복잡하죠? 어쨌든 주어진 조건들은 미지수들을 구하기에 충분하므로 이와 같은 방법으로 문제를 풀 수 없는 것은 아닙니다. 하지만 이렇게 거의 전적으로 대수학적인 접근을 취한다면 대량의 계산을 해야 하기에 시간이 많이 걸릴뿐더러, 여러 미지수들을 하나씩 찾는 과정에서 실수가 발생할 가능성도 작지 않습니다. 게다가 어떤 미지수를 어떤 미지수로 표현할지를 정하고, 또 어떤 미지수의 값을 먼저 정리할지 거듭 생각해야 합니다. 그리고 우여곡절 끝에 19번 문제를 맞힌다고 한들 수학 중간고사에서 19번 문제만 풀면 되는 게 아닌 이상, 앞서 쓴 바와 같이 시험시간 운용에 차질이 발생하기 십상입니다.
제목에서 중학교 수학의 중요성을 언급했던 까닭은, 실상 여태껏 설명한 난관이 중학교 때 수학 공부를 착실히 하는 것만으로 눈 녹듯 사라질 수 있었기 때문입니다. 더 구체적으로 밝히자면 중하교 2학년 때 ‘도형의 닮음’ 단원에서 배우고 익힌 것을 착실히 간직하고 있었더라면, 상문고 1학년 중간고사의 19번 문제를 가뿐하게 푼 뒤 나머지 문제들에 충분한 시간을 할애할 수 있었습니다.
문제에서 점 O, Q, P는 모두 일직선상에 있습니다. 즉. 삼각형 OIQ와 삼각형 OHP가 닮음이라는 뜻입니다. 또 삼각형 OIQ와 사각형 IHPQ의 넓이의 비가 1:8이라는 것은 곧 삼각형 OIQ와 삼각형 OHP의 비가 1:9라는 것을 의미합니다. 이때 닮은 도형의 넓이의 비는 닮음비의 제곱이므로, 선분 OI와 선분 OH의 길이의 비는 1:3이라는 것을 알 수 있습니다. 이후 q의 값은 k, p의 값은 3k로 두고 문제를 풀어나가면 됩니다.
q=k, p=3k라는 정리에 다다르는 데는 손을 움직일 필요도 없습니다. 눈썰미가 좋은 학생이었다면 이미 머릿속에서 몇 초 만에 정리가 끝났을 것입니다. 그다음부터 대수학적 접근을 하면 문제풀이가 가뿐해집니다. 이렇듯 발상에만 성공한다면, 19번 문제는 최소한의 계산을 통해 빠르게 정답을 도출할 수 있는 문항이었습니다.
상당수의 학생들, 특히 문과 진학을 희망하는 학생들은 기하학적 접근에 약한 모습을 보입니다. 하지만 상문고 수학 중간고사에 마음 편히 임할 수 있도록 하는 기하학적 접근이란 고교 과정에서 선택 과목으로 배우는 심화된 기하학 지식을 요구하는 것이 아니라 이미 중학교 때 배운 쉬운 내용이었습니다. 그럼에도 불구하고, 고등학교에서 별도로 기하학을 공부하지 않는 많은 학생들은 기하학적 접근을 시도할 생각조차 못하는 경우가 태반입니다.
이런 일이 발생하는 원인은 궁극적으로 기초에 충실하도록 하는 학습 태도를 기르지 못했기 때문입니다. 수학은 이미 배운 개념을 토대로 그것을 심화, 확장, 적용하는 중층적 특성이 지대한 과목인 고로, 기초에 충실하지 못한다면 성적에 적신호가 들어옵니다. 그리고 나름대로 공부를 잘하는 편이었던 학생들도 고등학교에 와서는 수학 성적이 하락하는 일이 자주 있습니다. 그것은 특별히 고등학교 수학이 어려워서가 아닙니다. 중학교에서 제대로 다지지 못한 기초로부터 유발되는 한계가 드러날 뿐입니다.
다행히도, 아직 고1인 학생들에게는 수학 실력을 끈기 있게 쌓아 올릴 많은 사건아 남아 있습니다. 하지만 올바른 학습 방법을 배우고 그 방법대로 공부하는 훈련을 반복함으로써 배운 내용이 철저하게 자기화되지 않는다면, 딴에는 노력했다고 한들 성적의 위기는 언제든 찾아올 것입니다. 이렇듯 안타까운 결과를 방지하고자 하는 마음이 여러 멘토들의 활동 동기 중 하나입니다.